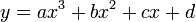AJUSTE DE CURVAS
El ajuste de curvas consiste en encontrar una curva que contenga una serie de puntos y que posiblemente cumpla una serie de restricciones adicionales. Esta sección es una introducción tanto a la interpolación (cuando se espera un ajuste exacto a determinadas restricciones) y al ajuste de curvas/análisis de regresión (cuando se permite una aproximación).
Ajuste de líneas y curvas polinómicas a puntos
Empecemos con una ecuación polinómica de primer grado:
Esta línea tiene pendiente a. Sabemos que habrá una línea conectando dos puntos cualesquiera. Por tanto, una ecuación polinómica de primer grado es un ajuste perfecto entre dos puntos.
Si aumentamos el orden de la ecuación a la de un polinomio de segundo grado, obtenemos:
Esto se ajustará exactamente a tres puntos. Si aumentamos el orden de la ecuación a la de un polinomio de tercer grado, obtenemos:
que se ajustará a cuatro puntos.
Una forma más general de decirlo es que se ajustará exactamente a cuatro restricciones. Cada restricción puede ser un punto, un ángulo o una curvatura (que es el recíproco del radio, o 1/R). Las restricciones de ángulo y curvatura se suelen añadir a los extremos de una curva, y en tales casos se les llama condiciones finales. A menudo se usan condiciones finales idénticas para asegurar una transición suave entre curvas polinómicas contenidas en una única spline. También se pueden añadir restricciones de orden alto, como "el cambio en la tasa de curvatura". Esto, por ejemplo, sería útil en diseños de intercambios en trébol para incorporaciones a autopistas, para entender las fuerzas a las que somete a un vehículo y poder establecer límites razonables de velocidad.
Si tenemos más de n + 1 restricciones (siendo n el grado del polinomio), aún podemos hacer pasar la curva polinómica por ellas. No es seguro que vaya a existir un ajuste exacto a todas ellas (pero podría suceder, por ejemplo, en el caso de un polinomio de primer grado que se ajusta a tres puntos colineales). En general, sin embargo, se necesita algún método para evaluar cada aproximación. El método de mínimos cuadrados es una manera de comparar las desviaciones.
Ahora bien, podríamos preguntarnos la razón de querer un ajuste aproximado cuando podríamos simplemente aumentar el grado de la ecuación polinómica para obtener un ajuste exacto. Existen varias:
- Incluso si existe un ajuste exacto, no quiere decir necesariamente que podamos encontrarlo. Dependiendo del algoritmo que se use, podríamos encontrar un caso divergente, donde no se podría calcular el ajuste exacto, o el coste computacional de encontrar la solución podría ser muy alto. De cualquier modo, tendríamos que acabar aceptando una solución aproximada.
- Quizá prefiramos el efecto de promediar datos cuestionables en una muestra, en lugar de distorsionar la curva para que se ajuste a ellos de forma exacta.
- Los polinomios de orden superior pueden oscilar mucho. Si hacemos pasar una curva por los puntos A y B, esperaríamos que la curva pase también cerca del punto medio entre A y B. Esto puede no suceder con curvas polinómicas de grados altos, ya que pueden tener valores de magnitud positiva o negativa muy grande. Con polinomios de grado bajo existen más posibilidades de que la curva pase cerca del punto medio (y queda garantizado que pasará exactamente por ahí, en los de primer grado).
- Los polinomios de orden bajo tienden a ser suaves y las curvas de los polinomios de orden alto tienden a ser "bulbosas". Para definir esto con más precisión, el número máximo de puntos de inflexión de una curva polinómica es n-2, donde n es el orden de la ecuación polinómica. Un punto de inflexión es el lugar de una curva donde cambia de radio positivo a negativo. Obsérvese que la "bulbosidad" de los polinomios de orden alto es sólo una posibilidad, ya que también pueden ser suaves, pero no existen garantías, al contrario que sucede con los polinomios de orden bajo. Un polinomio de grado quince podría tener, como máximo, trece puntos de inflexión, pero podría tener también doce, once, o cualquier número hasta cero.
Ahora que hemos hablado del uso de grados demasiado bajos para conseguir un ajuste exacto, comentemos qué sucede si el grado de una curva polinómica es mayor del necesario para dicho ajuste. Esto es malo por las razones comentadas anteriormente si los polinomios son de orden alto, pero también nos lleva a un caso en que exista un número infinito de soluciones. Por ejemplo, un polinomio de primer grado (una línea) restringido por un único punto, en lugar de los dos habituales, nos dará un número infinito de soluciones. Esto nos trae el problema de cómo comparar y escoger una solución única, lo que puede ser un problema tanto para humanos como para el software. Por esta razón es mejor escoger el polinomio de menor grado posible para obtener un ajuste exacto en todas las restricciones, y quizá incluso un grado menor si es aceptable una aproximación al ajuste.