sábado, 6 de octubre de 2012

ELIMINACIÓN DE GAUSS

 Eliminación gaussiana básica

Eliminación de Gauss-Jordan, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El metodo de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal unitaria.

Ilustraremos el método de Gauss aplicando el procedimiento a un sistema de cuatro ecuaciones con cuatro incógnitas:
 \begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 34 \\ 27 \\ -38 \end{array} \right) \end{array}\end{displaymath}
En el primer paso, multiplicamos la primera ecuación por $\frac{12}{6}=2$ y la restamos a la segunda, después multiplicamos la primera ecuación por $\frac{3}{6}=\frac{1}{2}$ y la restamos a la tercera y finalmente multiplicamos la primera ecuación por $\frac{-6}{6}=-1$ y la restamos a la cuarta. Los números 2, $\frac{1}{2}$ y -1 son los multiplicadores del primer paso del proceso de eliminación. El número 6 es el elemento pivote de este primer paso y la primera fila, que no sufre modificación alguna, se denomina fila pivote. El sistema en estos momentos tiene el siguiente aspecto:
 \begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 10 \\ 21 \\ -26 \end{array} \right) \end{array}\end{displaymath}
En el siguiente paso del proceso, la segunda fila se emplea como fila pivote y -4 como elemento pivote. Aplicamos del nuevo el proceso: multiplicamos la segunda fila por $\frac{-12}{-4}=3$ y la restamos de la tercera y después multiplicamos la segunda fila por $\frac{2}{-4}=-\frac{1}{2}$ y la restamos a la cuarta. Los multiplicadores son en esta ocasión 3 y $-\frac{1}{2}$ y el sistema de ecuaciones se reduce a:
 \begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 10 \\ -9 \\ -21 \end{array} \right) \end{array}\end{displaymath}
El último paso consiste en multiplicar la tercera ecuación por $\frac{4}{2}=2$ y restarla a la cuarta. El sistema resultante resulta ser:
 \begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ray}{r} 12 \\ 10 \\ -9 \\ -3 \end{array} \right) \end{array}\end{displaymath}
El sistema resultante es triangular superior y equivalente al sistema original (las soluciones de ambos sistemas coinciden). La solución del sistema de ecuaciones resulta ser:
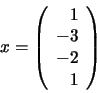
\begin{displaymath}x = \left( \begin{array}{r} 1 \\ -3 \\ -2 \\ 1 \end{array} \right) \end{displaymath}
Si colocamos los multiplicadores utilizados al transformar el sistema en una matriz triangular inferior unitaria (L) ocupando cada uno de ellos la posición del cero que contribuyó a producir, obtenemos la siguiente matriz:
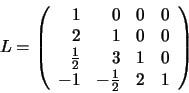
\begin{displaymath}L = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 2 & 1 & 0... ...& 3 & 1 & 0 \\ -1 & -\frac{1}{2} & 2 & 1 \end{array}\right) \end{displaymath}
Por otra parte, la matriz triangular superior (U) formada por los coeficientes resultantes tras aplicar el algoritmo de Gauss, es:
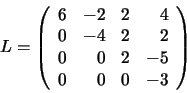
\begin{displaymath}L = \left( \begin{array}{rrrr} 6 & -2 & 2 & 4 \\ 0 & -4 &... ... 2 \\ 0 & 0 & 2 & -5 \\ 0 & 0 & 0 & -3 \end{array}\right) \end{displaymath}
Estas dos matrices nos dan la factorización LU de la matriz inicial de coeficientes, A.
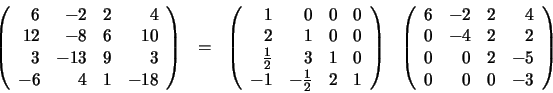
\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...0 & 2 & -5 \\ 0 & 0 & 0 & -3 \end{array} \right) \end{array}\end{displaymath}
Publicado por en

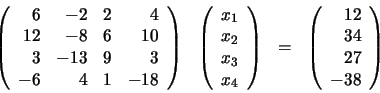
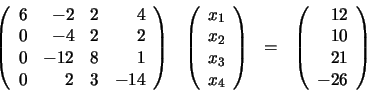
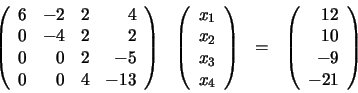
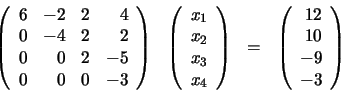
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)