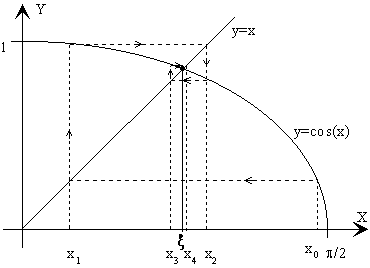
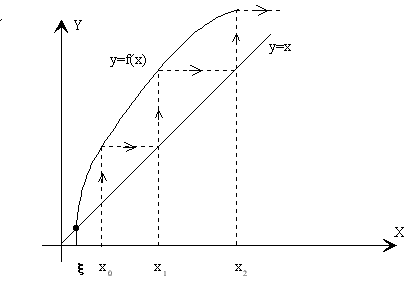
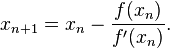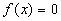MÉTODO DE BISECCIONES SUCESIVAS

MÉTODO DE BISECCIONES SUCESIVAS

El método de bisecciones sucesivas se genera de un intervalo donde al tabular  se genera un cambio de signo con el cambio de signo se llega a la conclusión de que allí se genera un raíz, en ese momento se genera un intervalo, normalmente se toma el valor anterior al cual esta cambiando de signo y el valor en donde cambio de signo por lo tanto debe cumplir.

f(x_a)f(x_b) < 0

Una ves ya obteniendo los dos valores x_{a y} x_b se genera un nuevo intervalo sumando

X_m= (x_a – x_b) / 2

ejemplo de la tabulación.

x	f(x)
xa	f(xa)     (+,-)
xm	f(xm)      + Significa que f(xm)f(xb) < 0               - Significa que f(xm)f(xb) < 0
xb	f(xb)     (+,-)

COMPROBANDO EL MÉTODO CON LA SIGUIENTE FUNCIÓN.

f(x)= x-cox(X)

Colocamos algunos valores (cuales quiera), estos valores son para que nos aproximemos a la raíz.

f(1)= 1 - cos(1) = 0.4596976941            

f(-1)= -1 - cos(-1) = -1.540302306        

Ahora calculamos el siguiente intervalo para acercarnos a la raíz, observar que los valores que obtuvimos son positivos y negativos (+,-).

X_m= ( -1+1 ) / 2 = 0

X	F(X)
-1	F(-1)= -1.540302306
0	F(0)= -1
1	F(1)=  0.4596976941

X_m= ( 0+1 ) / 2 = 0.5

X	F(X)
0	F(0)= -1
0.5	F(0.5)= -0.3775825619
1	F(1)= 0.4596976941

X_m= ( 0.5+1 ) / 2 = 0.75

X	F(X)
0.5	F(0.5)= -0.3775825619
0.75	F(0.75)= 0.01831113113
1	F(1)= 0.4596976941

X_m= ( 0.5+0.75 ) / 2 = 0.625

X	F(X)
0.5	F(0.5)= -0.3775825619
0.625	F(0.625)= -0.1859631195
0.75	F(0.75)= 0.01831113113

X_m= ( 0.625+0.75 ) / 2 = 0.6875

X	F(X)
0.625	F(0.625)=  -0.1859631195
0.6875	F(0.6875)= -0.08533494615
0.75	F(0.75)=  0.01831113113

X_m= ( 0.6875+0.625 ) / 2 = 0.71875

X	F(X)
0.6875	F(0.6875)= -0.08533494615
0.71875	F(0.71875)= -0.3333333337
0.625	F(0.625)=   -0.1859631195

Ejercicio 1. del Método Newton-Raphson

Ejemplo 1.

Consideremos el problema de encontrar un número positivo x tal que cos(x) = x³. Podríamos tratar de encontrar el cero de f(x) = cos(x) - x³.

Sabemos que f '(x) = -sin(x) - 3x². Ya que cos(x) ≤ 1 para todo x y x³ > 1 para x>1, deducimos que nuestro cero está entre 0 y 1. Comenzaremos probando con el valor inicialx₀ = 0,5

Los dígitos correctos están subrayados. En particular, x₆ es correcto para el número de decimales pedidos. Podemos ver que el número de dígitos correctos después de la coma se incrementa desde 2 (para x₃) a 5 y 10, ilustando la convergencia cuadrática.

MÉTODO DE NEWTON RAPHSON

MÉTODO DE NEWTON RAPHSON

En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson, o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.

• Descripción de Método

El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente. f'(x)= 0 Sea f : [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x₀ y definimos para cada número natural n

Donde f ' denota la derivada de f.

Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita cognoscible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.

La función ƒ es mostrada en azul y la línea tangente en rojo. Vemos que x_n+1 es una mejor aproximación que x_npara la raíz x de la función f.

MÉTODO DE ITERACION

MÉTODO DE ITERATIVO

En matemática computacional, un método iterativo trata de resolver un problema (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.

PUNTOS FIJOS ATRACTIVOS

Si una ecuación puede ponerse en la forma f(x) = x, y una solución x es un punto fijo atractivo de la función f, entonces puede empezar con un punto x₁ en la base de atracción de x, y sea x_n+1 = f(x_n) para n ≥ 1, y la secuencia {x_n}_n ≥ 1 convergerá a la solución x.

MÉTODO ITERATIVO ESTACIONARIO

Los métodos iterativos estacionarios resuelven un sistema lineal con un operador que se aproxima al original; y basándose en la medida de error (el residuo), desde una ecuación de corrección para la que se repite este proceso. Mientras que estos métodos son sencillos de derivar, implementar y analizar, la convergencia normalmente sólo está garantizada para una clase limitada de matrices.

Ejemplo de una aproximación sucesiva

EJEMPLO:

Un ejemplo típico es la de encontrar la raíz de la ecuación:

En la siguiente gráfica se observa como se va sacando la iteración de la ecuación: 

Para encontrar la raíz, se comienza en el punto cualquiera de abscisa x₀ dentro del intervalo (0, p/2), y se traza la línea vertical hasta que interseca la curva, luego, desde este punto, se traza una línea horizontal hasta que se alcanza la recta bisectriz, este punto tendrá por abscisa x₁. Se traza de nuevo, una línea vertical hasta encontrar a la curva, y otra línea horizontal hasta encontrar la línea recta, el punto de intersección tiene de abscisa x₂ , y así sucesivamente. Como podemos apreciar en la figura, la sucesión x₁, x₂, x₃... tiende hacia la raíz x de la ecuación buscada.

A continuación se muestra un ejercicio con la misma ecuación  hasta llegar a una aproximación de 0.001.

f(x)=x-cos(x)

g(x)=x=cos(x)

xn+1=cons(xn) hasta nmax=9, x0=0.5

n=0                                             n=1                                            n=2                         

x1=cos(x0)                                 x2=cos(x1)                                 x3=cos(x2)

x1=cos(0.5)                               x2=cos(0.878)                          x3=cos(0.639)

x1=0.8775825619                    x2=0.6386913466                  x3=0.8026925522

x1=0.878                                    x2=0.639                                  x3=0.803

x1=|x1-x0|=|0.878-0.500|           x2=|x2-x1|=|0.639-0.878|        x3=|x3-x2|=|0.803-0.639|

x1=0.378                                    x2=0.239                                  x3=0.164

 n=3                                             n=4                                            n=5                        

x4=cos(x3)                                 x5=cos(x4)                                x6=cos(x5)

x4=cos(0.803)                           x5=cos(0.695)                          x6=cos(0.768)

x4=0.6945515091                    x5=0.7680537018                   x6=0.7193015033

x4=0.695                                    x5=0.768                                  x6=0.719

x4=|x4-x3|=|0.695-0.803|          x5=|x5-x4|=|0.768-0.695|        x6=|x6-x5|=|0.719-0.768|

x4=0.108                                    x5=0.073                                  x6=0.049

n=6                                             n=7                                            n=8                         

x7=cos(x6)                                x8=cos(x7)                                x9=cos(x8)

x7=cos(0.719)                          x8=cos(0.752)                          x9=cos(0.730)

x7=0.7524647378                   x8=0.7303241289                   x9=0.7451744023

x7=0.752                                   x8=0.730                                  x9=0.745

x7=|x7-x6|=|0.752-0.719|         x8=|x8-x7|=|0.730-0.752|         x9=|x9-x8|=|0.745-0.730|

x7=0.033                                   x8=0.022                                  x9=0.015

Aun no se llega al resultado pero como se pueden dar cuenta no falta mucho así que con una o dos iteraciones mas se aproximara aun mas al resultado ideal.

Aproximaciones Sucesivas

APROXIMACIONES SUCESIVAS

El método de las aproximaciones sucesivas es uno de los procedimientos más importantes y más sencillos de codificar. Supongamos la ecuación

donde f(x) es una función continua que se desea determinar sus raíces reales. Se sustituye f(x) por la ecuación equivalente

Se estima el valor aproximado de la raíz x₀, y se sustituye en el segundo miembro de la ecuación para obtener x₁.

Poniendo x₁ como argumento de j(x), obtendremos un nuevo número x₂, y así sucesivamente. Este proceso se puede sintetizar en la fórmula.

 

Si esta secuencia es convergente es decir, tiende hacia un límite, la solución x es:

               

El criterio de convergencia

No todas las ecuaciones pueden resolverse por este método, solamente si el valor absoluto de la derivada de la función j(x) en la vecindad de la raíz x es menor que la unidad (la pendiente de la recta bisectriz del primer cuadrante es uno). En la figura, podemos ver como es imposible encontrar la solución marcada por un puntito negro en la intersección entre la curva y la recta bisectriz del primer cuadrante, ya que la sucesión x_i diverge.

   

Método de Aproximaciones

Aproximación es una representación inexacta que, sin embargo, es suficientemente fiel como para ser útil.

Aunque en matemáticas la aproximación típicamente se aplica a números, también puede aplicarse a objetos tales como las funciones matemáticas, figuras geométricas o leyes físicas.

Ejercicios

Ejercicio realizado en el salón de clase.

• Serie de Taylor 

En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto(a-r, a+r) se define como la siguiente suma:

La función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).

Aquí, n! es el factorial de n y f ⁽ⁿ⁾(a) indica la n-ésima derivada de f en el punto a.

Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.

Errores

Los métodos numéricos ofrecen soluciones aproximadas muy cercanas a las soluciones exactas; la discrepancia entre una solución verdadera y una aproximada constituye un error, por lo que es importante saber qué se entiende por aproximar y aprender a cuantificar los errores, para minimizarlos.

• Error Relativo 

Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas.
La relación entre un resultado exacto o verdadero X y el valor aproximado X* está dado por:

X = X* + error  

El que un error tenga signo positivo o negativo, generalmente no tiene importancia, de manera que el error absoluto se define como el valor absoluto de la diferencia entre el valor verdadero y el valor aproximado:

E = |X - X*|  

El error absoluto se expresa en las mismas unidades que X y no toma en cuenta el orden de magnitud de la cantidad que se está midiendo.

• Error absoluto

El error relativo normaliza el error absoluto respecto al valor verdadero de la cantidad medida:

e = |E/X| = |(X - X*)/X|

El error relativo es adimensional y puede quedar expresado así, en forma fraccional, o se puede multiplicar por 100 para expresarlo en términos porcentuales:

e (%) = |E/X| x 100

Ejemplo.

Este ejemplo se realizo en la clase que es e elevado a la uno.

• Error Inherente

Los errores inherentes se producen por la propia variabilidad de los fenómenos; al ser caracterizados a través de cantidades físicas, las mediciones  conllevan incertidumbre, pues los instrumentos de medición ofrecen sólo una aproximación numérica del valor verdadero de la magnitud medida, pues se calibran para considerar solamente un determinado número de cifras significativas.  Todas las magnitudes que se manejan en ingeniería son susceptibles a este tipo de errores.